Cygnus Biosciences
In this blog post I’m going to briefly review Chinese DNA sequencing start up Cygnus Biosciences. If you’re interest in other DNA Sequencing startups, check out my list of startups, which also links to relevant summary blog posts.
I enjoyed reading about the Cygnus approach and the error correcting scheme is entertaining for a comp. sci. like me. If you’re into information theory I recommend skipping past the business and chemistry sections, or just take a look at their 2017 paper [2] which describes the method in more detail (and has lots of cool figures).
Business
Cygnus Biosciences is a Beijing company founded in 2017. Reports state they have raise a series B round. However I can only find evidence of a single round taking place. Perhaps there was earlier grant funding, and due to its large size the 19.6M USD round is taken as a series B, it’s unclear.
Investors include Proxima Ventures Ltd, Beijing Longpan Investment Management Consulting Center, Zhongguancun Development Group, Shanghai Creation Investment Management Co Ltd, General Technology Venture Capital, and Beijing Jinggong Hongyuan Venture Capital Center [3]. All investors aside from Proxima appear to be based in China.
Technology
Cygnus appear to have two novel technologies at play. These are both covered in a single international patent [1], which claims priority to a few other Chinese patents (which I’ve not tried to track down). The patent is huge at 224 pages. It contains a lot of data, a lot of figures (pictures of wetting angles, schematics and graphs galore). I’ve not read it in any depth. The basic mechanisms seem to be more clearly described in their papers.
Sequencing Chemistry
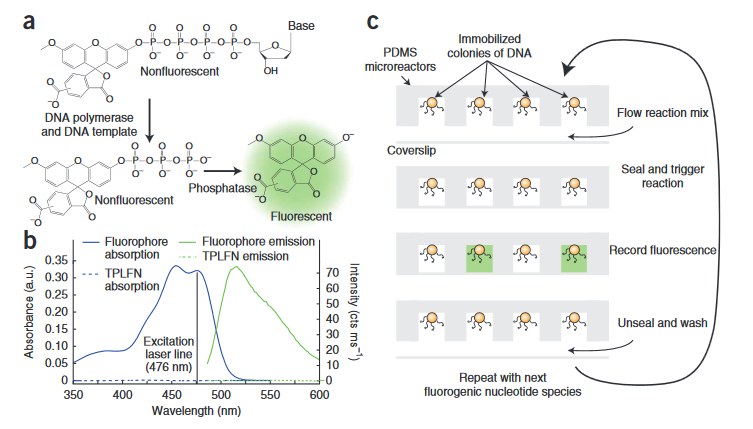
The sequencing chemistry was originally described in a 2011 paper from Harvard University [5].
In this system, non-fluorescent bases are introduced into the system. When these modified bases incorporate a fluorophore is released into solution and can be detected. Because the fluorophores are released into solution, the reaction and detection needs to take place in a sealed well with DNA immobilized on beads. The intensity of the fluorescence increases with the number of bases incorporated. As with all such un-terminated technologies there are likely issues with longer homopolymer runs.
Overall, this seems somewhat similar to 454s technology (which ultimately didn’t fare so well). The key difference here is the detection method. On 454s platform the signal was detected via a luciferase-catalyzed reaction. This reaction produced flashes of light that were detected by a camera. The wells therefore had to be monitored during incorporation. This meant it was impossible to have multiple imaging regions, which ultimately made it difficult to scale the throughput of the platform. Other platforms (Illumina) scaled better, and out-competed 454.
With the method presented by Cygnus, you can run the incorporation reaction and then detect the fluorescence at a later point. This means that rather than being limited by the size of your camera, you can just increase the chip size and scan the camera across it to increase throughput.
The original paper shows reads of around 30bp. The 2017 paper describing their error correction system shows much longer reads (200bp+). There isn’t much on the chemistry in the main paper, so it’s not clear what changes have been made. For those interested, it may be worth digging into the patent and supplementary info.
Error Correction Method
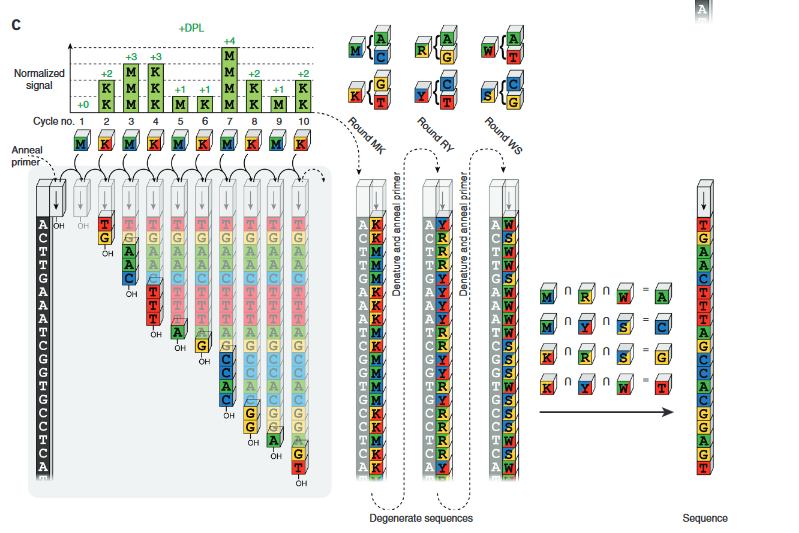
Cygnus also present an error correction method. The method can actually be applied to any un-terminated single channel SBS chemistry (Ion torrent, 454 etc.). Rather than detecting the incorporation of a single base type, the Cygnus system uses mixtures of multiple base types (as such it may be somewhat related to the Centrillion method). They then sequence the same template multiple times using different base mixes before computationally combining the reads to resolve the template sequence.
It’s a neat system, and it’s well illustrated in the paper:
You might well just want to refer to the description in their paper. But for my own benefit I’ve been playing with the method myself.
Conceptually we can imagine generating all possible unordered groups of 2 bases (AC, AG, AT, GT, CT and CG). These are going to be the base mixtures which will be used in the sequencing process.
To build our sequencing system using these mixtures we will obviously need more than one type of mixture. But let’s start with one. A mixture of G and T bases. We’ll call this the “K” group [4]. What will happen in the degenerate case where we have a AC repeat followed by a TG repeat i.e. ACACACACTGTGTGTG? Our read system will just tell us we incorporated the “K” mixture 8 times and then stop because there are no A or Cs in our mixture. So to process the whole strand we need to add second mixture, a mixture of A and C bases we’ll call this mixture the “M” group.
If we alternate between incorporating “K”s and “M”s our read system will tell us we have 8 Ks followed by 8 Ms. Not very useful as a sequencing platform…
In order to resolve this ambiguous read we add read the same strand of DNA again, but this time use a different mixture of bases. Which groups? Well we want to be able to determine which of the two “K” bases was incorporated and which of the two “M” bases was incorporated.
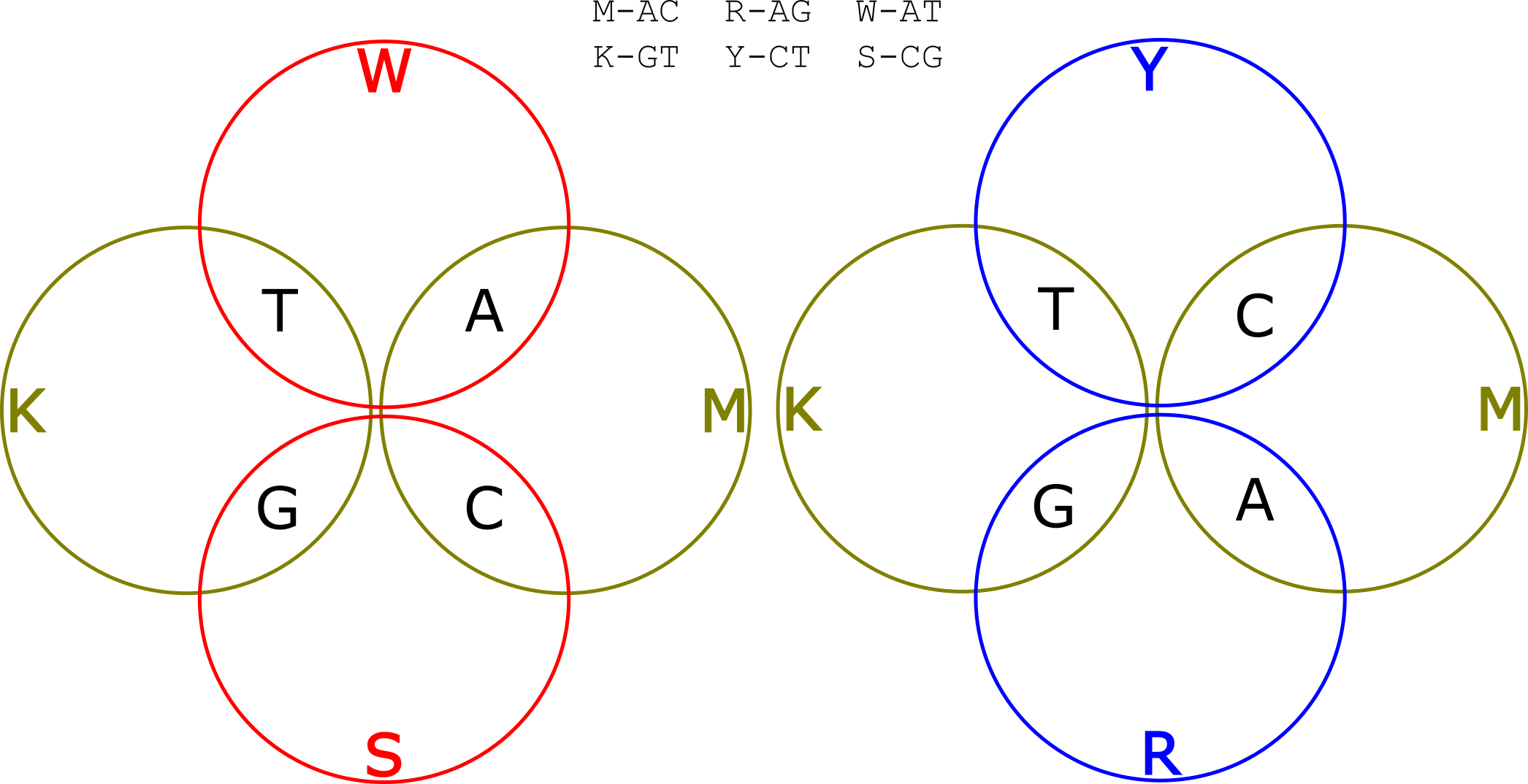
There are actually two different ways of doing this. We can either use alternating mixtures of A/T and C/G (let’s call them W and S groups) or mixtures of A/G and C/T (R and Y). These two alternatives are illustrated in the Venn diagrams below:
Let’s say we use the W and S groups. So we have one read, where we alternated incorporating K and M mixtures, and another where we alternated incorporating W and S mixtures. Our template was ACACACACTGTGTGTG. So the KM read is: KKKKKKKKMMMMMMMM. The WS read is: WSWSWSWSWSWSWSWS. Now let’s deconvolve the read.
Our first base is in groups K and W, only G is in both groups K and W, so our first basecall is a C. Our second base is in groups K and S, only G is in groups K and S so must have incorporated a G and we call a T. Proceeding in this manor we can uniquely identify the base at each position in the template.
So with two reads using alternating mixtures of two different types we can completely resolve the original template. Neat! We’ve used more sequencing, but only two more incorporations (more about this later).
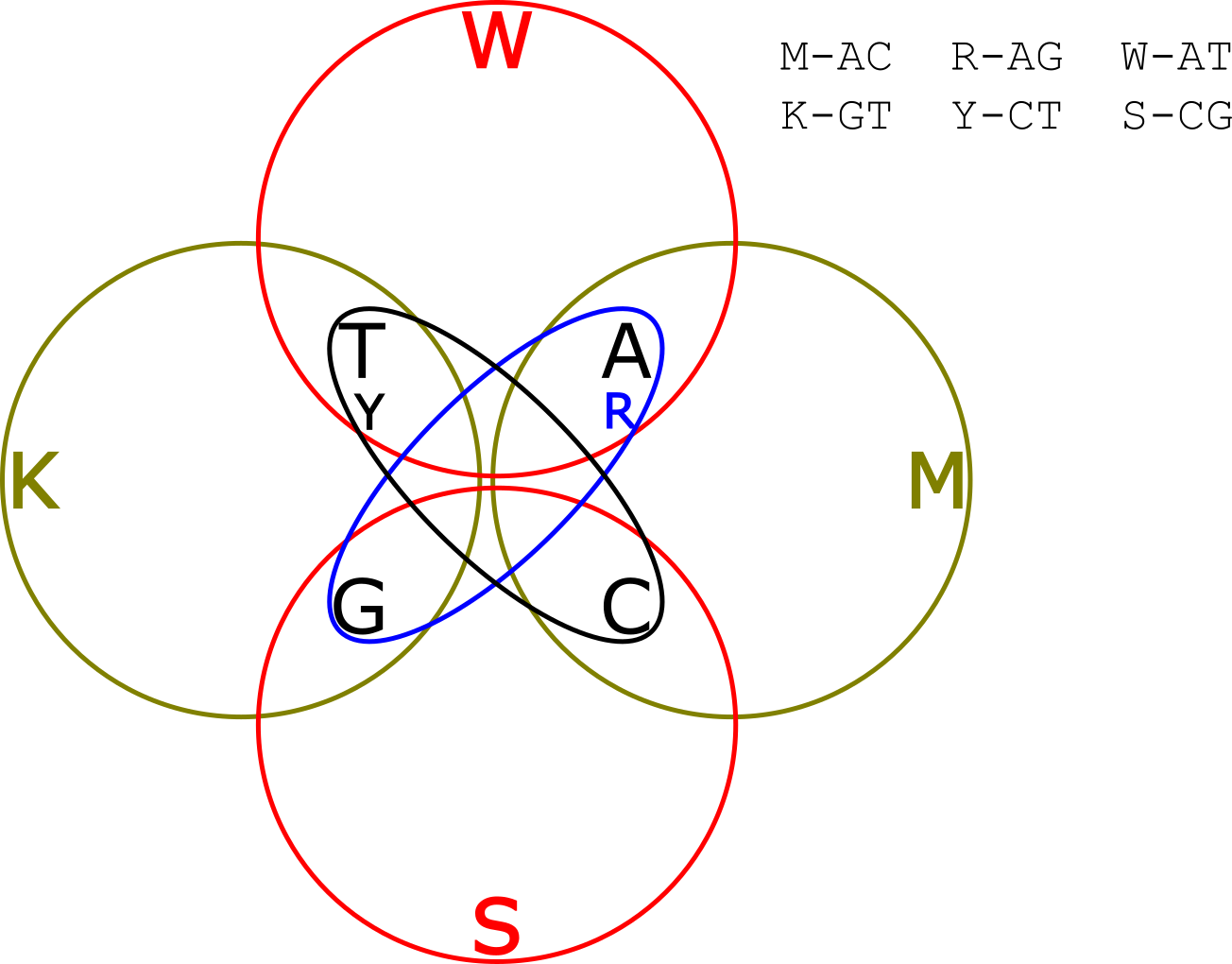
But wait! What was the point? We’ve just sequencing the template, we could have done that without any of this mixture stuff. Well…why stop at 2 sub-reads? Why not add a third and see if that provides any extra value? Remember we had two options in our Venn diagram above for deconvolving the original read? We can add the other 2 groups into our Venn diagram and create this crazy thing:
OK, so now you’re reading each template 3 times. There is obviously redundant information. So if your reads indicated that the first base was in groups “TG” “CT” and “AT” you only need two out of three groups to know that T is the only common member, and that you should call and A. But it your reads indicate that the first base was in groups “TG” “CT” and “GC” clearly something is wrong. There are two groups with each of T,G and C in them. We can’t resolve the base at this position, but we do know something went wrong and can call an ambiguity (“N” base) at this point, preventing the error from effecting downstream analysis.
In general however, errors are unlikely to be of this type. What’s more likely is that a run length is likely to be miscalled. So 3 “W”s in a row will be called instead of 4. These types of errors can not just be detected under this encoding, but also corrected.
The paper claims that they can reduce error rates on their platform from 0.96% to 0.33%. I mentioned previously that more sequencing was required. However, this is only true in the degenerate case. In a normal single channel SBS system you don’t generally incorporate a base every cycle (or flow in Ion torrent jargon). In this system you always do and on average the paper suggests that say 2 bases are incorporated per cycle as opposed to 0.67 bases on other platforms. However, there are clearly degenerate cases (or low complexity cases) where this is not true so the system relies on the template being more or less random (I’d be curious to know what would happen in a high CG content template for example).
Overall, the error correction system seems like a neat idea. It will be interesting to see how it compares to reversible-terminate chemistries like Illumina’s in practice.
Notes
[1] Patent:
https://patentscope.wipo.int/search/ko/detail.jsf;jsessionid=E1CFF0A5F71C9CCAF85848F1A54CA650.wapp1nA?docId=WO2017084580&recNum=692&office=&queryString=&prevFilter=&sortOption=%EA%B3%B5%EA%B0%9C%EC%9D%BC%28%EB%82%B4%EB%A6%BC%EC%B0%A8%EC%88%9C%29&maxRec=3070432
Click to access WO2017084580A1.pdf
[2] Nature Biotechnology Paper: https://bernstein.harvard.edu/papers/2017_Chen_NBT.pdf
[3] https://www.crunchbase.com/organization/cygnus-biosciences#section-funding-rounds
[4] These are the group identifiers used in the IUPAC ambiguity codes: http://www.dnabaser.com/articles/IUPAC%20ambiguity%20codes.html
[5] https://bernstein.harvard.edu/papers/NAT%20METHODS%20v8%20575-80%20JUL%202011%20SIMS.pdf