A Brief Computational Analysis of “Pen-Pineapple Apple-pen”
Pen-Pineapple Apple-pen is the latest earworm [1] out of Japan. It has deceptively simple lyrics [3]. Starting with the refrain:
I have a pen. I have an apple. Ungh Apple-pen.
What makes the lyrics interesting, is the way he plays with word ordering [4]. First mentioning Pen, then Apple before switching it around to become Apple-pen. I think it’s this reordering which engages the brain and helps give the song its memetic qualities.
The lyrics continue, repeating the process with Pen-pineapple, finally generating the string:
Pen-pineapple Apple-pen.
Piko-Taro then compresses this into the 2 symbol alphabet: PPAP. However, as “pineapple” contains “apple” we could expand this to: PPAAP.
PPAAP is a rather interesting string. Let’s look at every 2 symbol substring:
PP PA AA AP
There are 4 possible 2 symbol strings over this alphabet, and each one is represented exactly once in the string PPAAP. It’s interesting to note that this would not have happened if Piko-Taro had chosen a different ordering, for example APPPA (Apple-Pen Pen-Pineapple) would give us 2 repeats of the substring PP and no occurrence of AA [5].
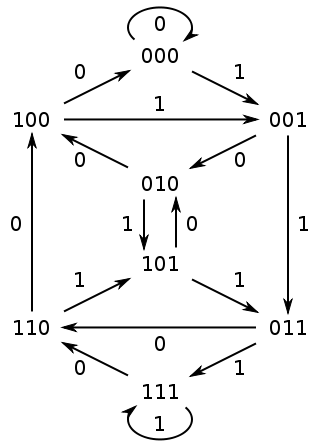
Strings that contain every substring of a given length (n) over a given alphabet (size k) are called De-Bruijn sequences. In order to create DeBruijn sequences, we generally start with a graph [6]:
The graph [7] has a vertex labeled with each string of length n-1 (in this case 1). Edges then connect the vertex to the vertex labeled with the suffix (of length n-1) of the string that would be created by adding the symbol the edge is labeled with.
To generate debruijn sequences from this graph we need to find Eulerian cycles in the Debruijn graph. That is to say, we need to visit each edge once before returning to the starting point. The starting vertex label, followed by the edge labels forms the DeBruijn sequence.
The PPAAP graph is of course trivial, and we can easily spot the 2 valid Debruijn sequences: PPAAP and AAPPA.
Debruijn sequences however get steadily more complex, lets take a look at one example from the wikipedia page:
Which is the Debruijn graph for n=4 k=2. From this we can generate the sequence 0000111101100101. Or in the PA alphabet: PPPPAAAAPAAPPAPA using the P=pen, PA=pineapple A=apple mapping:
Pen-pen-pen-Pineapple-apple-apple-apple-pineapple-apple-pen-pineapple-pineapple
Which I assume will form the basis of Piko-Taro’s next video.
If you like this kind of inane rambling. You should probably follow me on twitter or consider hiring me, where I will attempt to rambling consistently on the topic of your choice.
[1] Historically known as a maggot.
[2] Interesting, while the Japanese transliterated subtitled reflect what he actually says in the video. The english version of these is incorrect in some-places (or perhaps there is some deeper hidden stringological meaning).
[3]
PPAP
I have a pen. I have an apple. Ungh Apple-pen. I have a pen. I have pineapple.
Ungh
Pineapple-pen.
Apple-pen.
Pineapple-pen.
Pen-pineapple-apple-pen.
Pen-pineapple-apple-pen. [2]
[4] Something that English speakers at least have an intuitive feel for.
[5] Many years ago I wrote some tools for calculating repeat counts in string efficiently. The repeat structure of string is often, interesting, informative, and beautiful. However there’s no money in it, and I don’t do it anymore. 🙂
[6] Interestingly, over the past few users sparse DeBruijn graphs have found applications in the assembly of DNA reads into more complete genomic sequences.
[7] I used the excellent tkz-graph with Latex to create this graph.
RSS