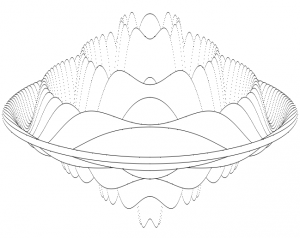
I was looking through an old copy of Beebug from 1982 and came across a review for “Practical Programs for the BBC Computer and Acorn Atom”:

The review contains a code listing from the book to draw a “very nice 3D object”. I decided it might be fun to port the program to HTML5 using a canvas. I also modified it slightly to animate the rendering. It’s a direct port, I just ported it line for line and then added code to vary YS to animate the object. Click below to take a look:
CLICK TO OPEN ANIMATION
opens in new window
The basic html5 implementation was pretty straightforward, however getting it to animate without a horrible amount of flickering was harder. It doesn’t look like canvas has support for double buffering, the only option being to use 2 canvas objects and hide one while you’re drawing to it. Blanking the whole canvas resulted in a horrible flicker for me, so instead I opted to black vertical lines during the rendering of each frame, this seems to work pretty well.
If you liked this thing, there’s another one here.
Notes
Here’s the full text of the article:
Title: Practical Programs for the BBC Computer and Acorn Atom
By: David Johnson-Davis Price £5.95
Reviewer: David Graham
As its title suggests, this book is not concerned with teaching you to program, or with teaching you to use the computer, but with the presentation of a number of programs. The range of programs offered is good, and includes games, graphics, number and word handling, and rather surprisingly an SPL compiler. With each program there is a discussion of the objects and principles involved (though nothing on the programming principles). The program listings are also broken down into useful subsections with boxed functional headings. This makes them relatively easy to follow.
The final section of the book, chapter 5, introduces the subject of compilers, and gives a listing for an experimental Simple Programming Language compiler for the BBC machine, plus a number of SPL programs that may be run on it. This all looks very interesting, and well worth some closer study. But if you are not interested in compilers, you are left with only 65 pages of the book; and since some of that space is taken up with the Acorn Atom version of each program presented, the book becomes a little expensive per useable page. It does, however, contain some good ideas, such as the brief program given below which plots the very nice 3D object in the photograph.
10 REM FROM:
20 REM PRACTICAL PROGRAMS FOR THE
30 REM BBC COMPUTER AND ACORN ATOM
40 REM BY DAVID JOHNSON-DAVIS
50 MODE4:VDU29,640,512;:XS=4:YS=4
60 A=640:B=A*A:C=512
70 FORX=0TOA STEPXS:S=X*X:P=SQR(B-S)
80 FORI=-P TO P STEP 6*YS
90 R=SQR(S+I*I)/A
100 Q=(R-1)*SIN(24*R)
110 Y=I/3+Q*C
120 IFI=-P THEN M=Y:GOTO150
130 IFY>M M=Y: GOTO160
140 IFY>=N GOTO170
150 N=Y
160 PLOT69,-X,Y:PLOT69,X,Y
170 NEXT:NEXT
180 END
The Javascript:
function draw_frame() {
var canvas = document.getElementById("m_canvas");
if(canvas.getContext) {
var ctx = canvas.getContext("2d");
ctx.lineWidth = 0;
ctx.fillStyle = "rgb(0,0,0)";
var size=1;
var offset=0;
ctx.scale(1,-1);
var xs=2;
var ys=ittr;
var a=640;
var b=a*a;
var c=512;
for(var x=0;x<=a;x=x+xs) {
s = x*x;
p = Math.sqrt(b-s);
ctx.clearRect((( x+640)/2)+offset,0,2,canvas.height);
ctx.clearRect(((0-x+640)/2)+offset-1,0,2,canvas.height);
// size=0.5; offset=0;
for(var i=0-p;i<=p;i+=6*ys) {
var r = Math.sqrt(s+i*i)/a;
var q = (r-1)*Math.sin(24*r);
y = i/3 + q*c;
if(i==0-p) {m=y; n=y; ctx.fillRect(((0-x+640)/2)+offset,(512-(y+512)/2)+offset,size,size); ctx.fillRect(((x+640)/2)+offset,(512-(y+512)/2)+offset,size,size); }
if(y>m) {m=y; ctx.fillRect(((0-x+640)/2)+offset,(512-(y+512)/2)+offset,size,size); ctx.fillRect(((x+640)/2)+offset,(512-(y+512)/2)+offset,size,size); }
if(!(y>=n)){n=y; ctx.fillRect(((0-x+640)/2)+offset,(512-(y+512)/2)+offset,size,size); ctx.fillRect(((x+640)/2)+offset,(512-(y+512)/2)+offset,size,size); }
}
}
ittr = ittr + delta;
if(ittr < 0.6) delta = 0-delta;
if(ittr > 100) delta = 0-delta;
}
}
The function is then triggered by a setInterval on the page load as follows:
<body onload="setInterval(draw_frame,10);" >
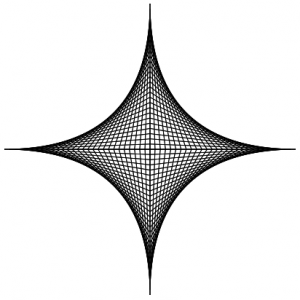 Click Here to open in new window.
Click Here to open in new window.
